Tufts University

    The ongoing research projects that cover the following areas:
  • Complex fluids and materials
  • Active condensed matter
  • Liquid crystal physics
  • Nonlinear elasticity
  • Fluid-structure interaction
  • Soft robotics
  • Biological flows and biomedicine
  • High performance computing 

1.  Soft colloids
Microscopic soft particles are commonly found in nature and engineeringapplications. Examples include red blood cells, fluid vesicles and microgel particles. When placed in a liquid, soft particles can readily undergo large deformations to accommodate the hydrodynamic forces, which in turn has a significant impact on the macroscopic rheological properties of the mixture.
* Shear rheology   We consider a suspension of elastic solid particles in a viscous liquid. The particles are assumed to be neo-Hookean and can undergo finite deformation. When placed in a shear flow, three types of motion - steady-state, trembling and tumbling - are found. The rheological properties generally exhibit shear-thinning behavior, and can even show negative intrinsic viscosity for sufficiently soft particles.
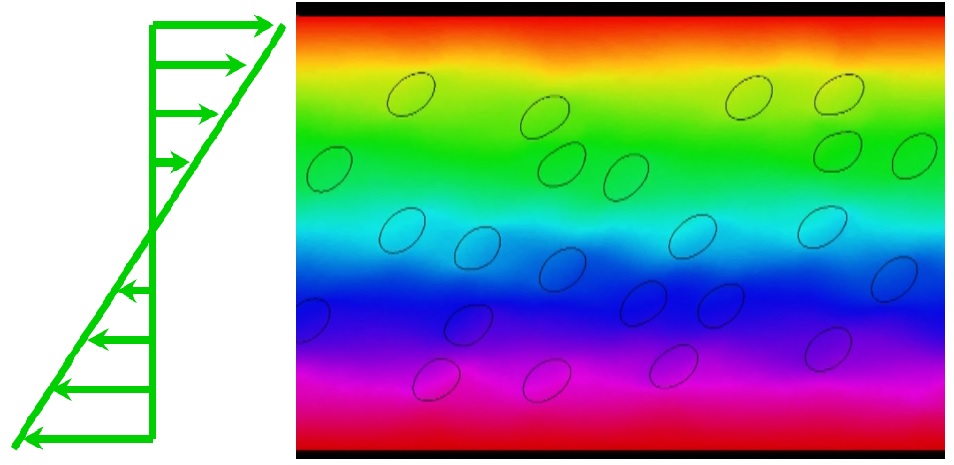
Fig 1: Suspension of deformable particles under simple shear ( Gao et al. 2011).
* Critical behaviors of polymer dynamics   We examine the underlying physical mechanisms of microdynamics of polymers when subjected to viscous fluid forces. For example, we study the phenomenon of the ‘coil-stretch’ (C-S) transition, wherein a long-chain polymer initially in a coiled state undergoes a sudden configuration change to become fully stretched under steady elongational flows. We introduce a continuum model in this study to investigate the C-S transition in a constant uniaxial elongational flow. Our approach involves approximating the unfolding process of the polymer chain as an axisymmetric deformation of an elastic particle.
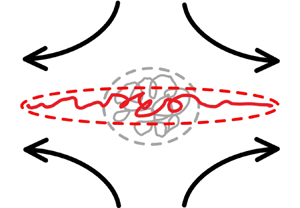
Fig 2: Coil-stretch transition of long-chain polymer ( Gao 2024 ).
* Electrohydrodynamics   We study the dynamics of a long elastic particle undergoing electrophoresis. The particle is elliptical in shape and is initially aligned with its major axis perpendicular to the direction of a uniformly applied electric field. The particle tends to curl up at its ends and arches in the middle. After a transient deformation, the particle migrates at Helmholtz-Smoluchowski velocity.
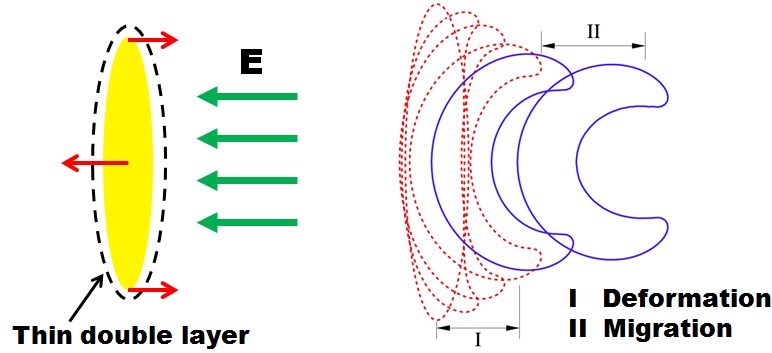
Fig 3: Electrophoresis of soft ellipsoidal particle ( T. Swaminathan et al. 2010 ).
2.  Active condensed matter
As a new branch of complex fluids, active matter is composed of self-driven constitutes with emergence of nonequilibrium physics. Despite the difference in composition, all these active systems orchestrate cooperative actions across various length and time scales, accompanying energy conversion from one form (e.g., chemical fuel) to another (e.g., mechanical work). Typical systems include cytoskeletal networks, synthetic microswimmers, bacterial suspensions, etc.
* Bacteria and algae   Active suspensions of swimming microorganisms, such as bacteria or algae, can exhibit fascinating collective behaviors that feature large-scale coherent structures, enhanced mixing, ordering transition, and anomalous diffusion. Even in the limit of vanishing Reynolds numbers, densely packed self-driven or swimming micro-particles effectively exert stresses upon the ambient liquid to act as a coupling medium for the generation of active flows via instability concatenations to amplify the disturbances due to particle motions and local (e.g., steric) interactions. We build a computation model, including the high-fidelity particle simulator and bottom-up continuum models, to study the non-equilibrium physics of suspensions of rear- and front-actuated microswimmers, or respectively the so-called “pusher” and “puller” particles. .
Fig 4: Direct particle simulations for spherical pullers (e.g., microalgae, ( Lin and Gao 2019 ) and rod-like pushers (e.g., E. Coli).
* Active cellular matter   Microtubules and motor-proteins are the building blocks of self-organized subcellular structures such as the mitotic spindle and the centrosomal microtubule array. They are ingredients in new "bioactive" liquid-crystalline fluids that are powered by ATP, and driven out of equilibrium by motor-protein activity to display complex flows and defect dynamics. We develop a multiscale theory for such systems. Brownian dynamics simulations of polar microtubule ensembles, driven by active crosslinks, are used to study microscopic organization and the stresses created by microtubule interactions. This identifies two polar-specific sources of active destabilizing stress: polarity-sorting and crosslink relaxation. We develop a Doi-Onsager theory that captures polarity sorting, and the hydrodynamic flows generated by polar-specific active stresses. In simulating experiments of active flows on immersed surfaces, the model exhibits turbulent dynamics and continuous generation and annihilation of disclination defects. Analysis shows that the dynamics follows from two linear instabilities, and gives characteristic length- and time-scales.
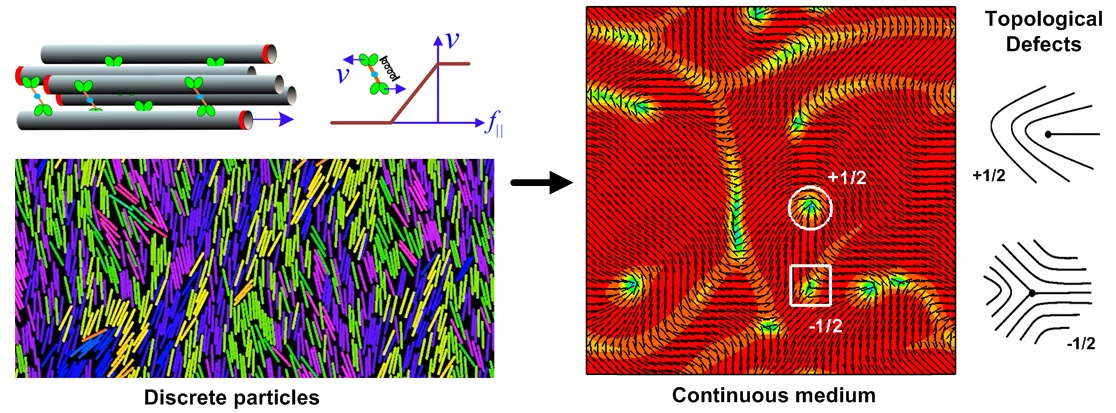
Fig 5: Multiscale analysis of motor-connected MT assemblies with hydrodynamics ( Gao et al. 2015 ).
* Geometric control and manipulation   To effectively control the collective dynamics in various internally-driven systems, it is critical to manipulate the emergent coherent structures. One way of doing this is to tune the suspension concentration and the amount of chemical fuels. Alternatively, we can take advantage of the particle interactions, either individually or collectively, with obstacles and geometric boundaries to manipulate the system more directly. By trapping active suspensions (such as Pusher swimmers or Quincke rollers) within the straight and curved boundaries, stable flow patterns, such as unidirectional circulations, traveling waves, density shocks, and rotating vortices, have already been constructed. More interestingly, active nematic flows under soft confinement by surface tension are able to generate internal flows to break symmetry and drive the whole-body movement.
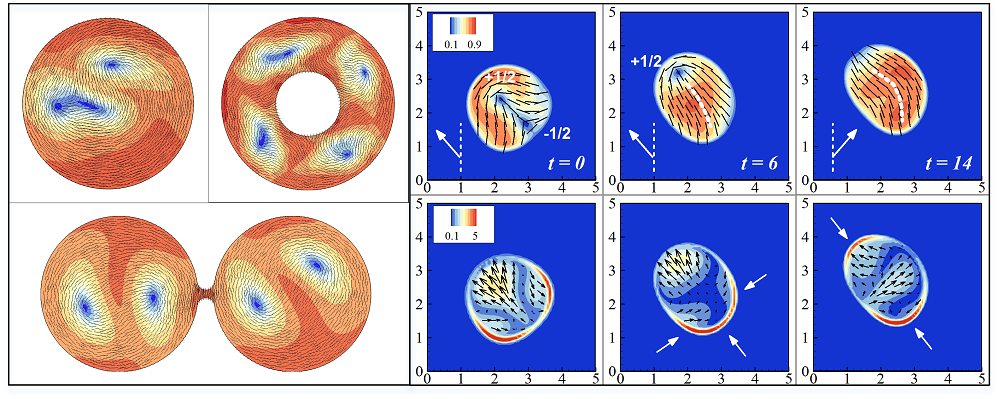
Fig 6: Generation of topological defects under the rigid ( Chen et al. 2018 ) and soft ( Gao and Li 2017 ) confinement.
3.  Soft robotics
Soft robotics is an emerging area that draws extensive interests from core areas in materials science and engineering, human health and medicine, applied mathematics, and biomechanics. It stimulates new structural design, and has advantages of simple control, light-weight, miniaturization, and affordable rapid fabrication. Compared to the conventional robots that are often made of rigid parts, the soft robots that are made from deformable materials can undergo flexible deformation under actuation, which essentially permits infinite degrees of freedom to facilitate complicated operations.
* Inertial swimmer   Designing soft swimming robots that actively deform in fluids is challenging. Fast swimming requires significant momentum exchange between the robot and fluid to overcome viscous drag, demanding rapid, stable, and reversible deformations. Efficient locomotion also depends on specific swimming gaits that exploit thrust from drag and wake effects—especially important at low or moderate Reynolds numbers where viscosity dominates. Understanding these dynamics requires jointly analyzing robot geometry, material properties, actuation strategies, and fluid interactions. Lightweight structures can also experience instabilities in fluid, complicating control. Although many soft robots have been built and tested, fully understanding their propulsion still requires combining experiments with accurate modeling and simulation.
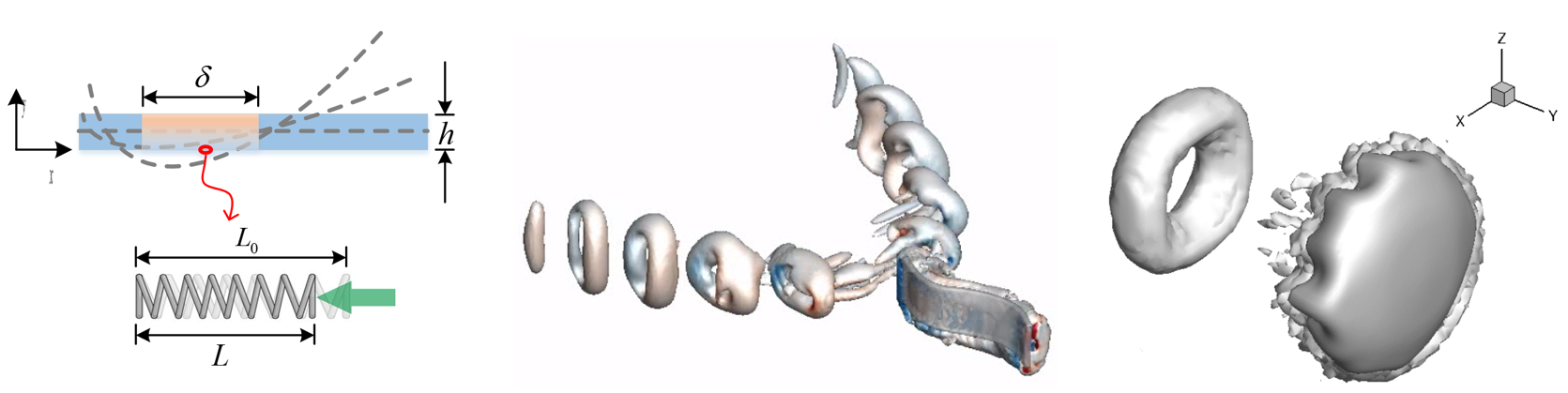
Fig 7: Bioinspired design for soft swimming robots (fish and jellyfish, Lin et al. 2019 ) powered by active strain.
* Non-inertial swimmer and microfluidics   Many organisms live in microfluidic environments, either biological or synthetic, where the fluid inertia is negligible. In the so-called Stokes (or creeping) flows, Purcell’s scallop theorem explains that performing time-reversible motions cannot generate directional swimming or locomotion owing to kinematic reversibility. We design a computational framework for studying the undulatory motion of a finite-length biomedical robots, i.e., microrobots, in a solution of liquid crystal polymers, a class of rigid, rodlike aromatic polymers that have much larger sizes and higher aspect ratios than small molecules (e.g. para-azoxyanisole). Our numerical and theoretical studies suggests the undulatory swimmers are in favor of aligning with the background nematic polymer structures.
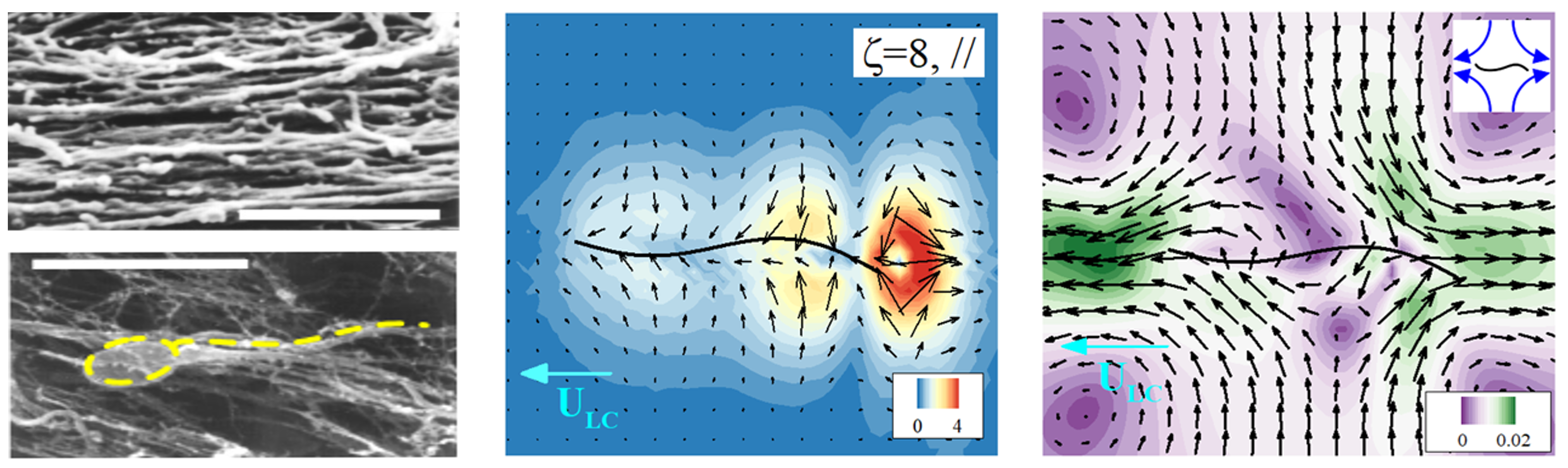
Fig 8: Undulatory micro soft swimmers like spermatozoa prefer to align with the background polymer structures while navigating in anisotropic complex fluids ( Lin et al. 2022 ).
4.  Cardiac mechanics and patient specific model
The heart is a highly complex living structure whose primary function is to cyclically contract in order to generate a pressure gradient to perfuse all body organs including itself. To do so, however, the heart behaves an integrated system where all components of the operation, such as excitation contraction coupling, are tightly orchestrated. Heart failure often develops when one component fails or when the components are not operating synchronously. Computational modeling has been useful in developing understanding and generate hypothesis concerning the heart function, diseases and treatments. The recent advancement in HPC and patient specific models also include detail FSI between blood flow and the mechanics of the heart wall, which hence provide more accurate physical mechanisms for cardiac systems.
* Cryoballoon ablation   Cryoballoon ablation (CBA) is a cryo-energy based minimally invasive treatment procedure for patients suffering from left atrial (LA) fibrillation. Although this technique has proved to be effective, it is prone to reoccurrences and some serious thermal complications. We describe the development of a thermal-hemodynamics computational framework to simulate incomplete occlusion in a patient-specific LA geometry during CBA. The modeling framework uses the finite element method to predict hemodynamics, thermal distribution, and lesion formation during CBA.
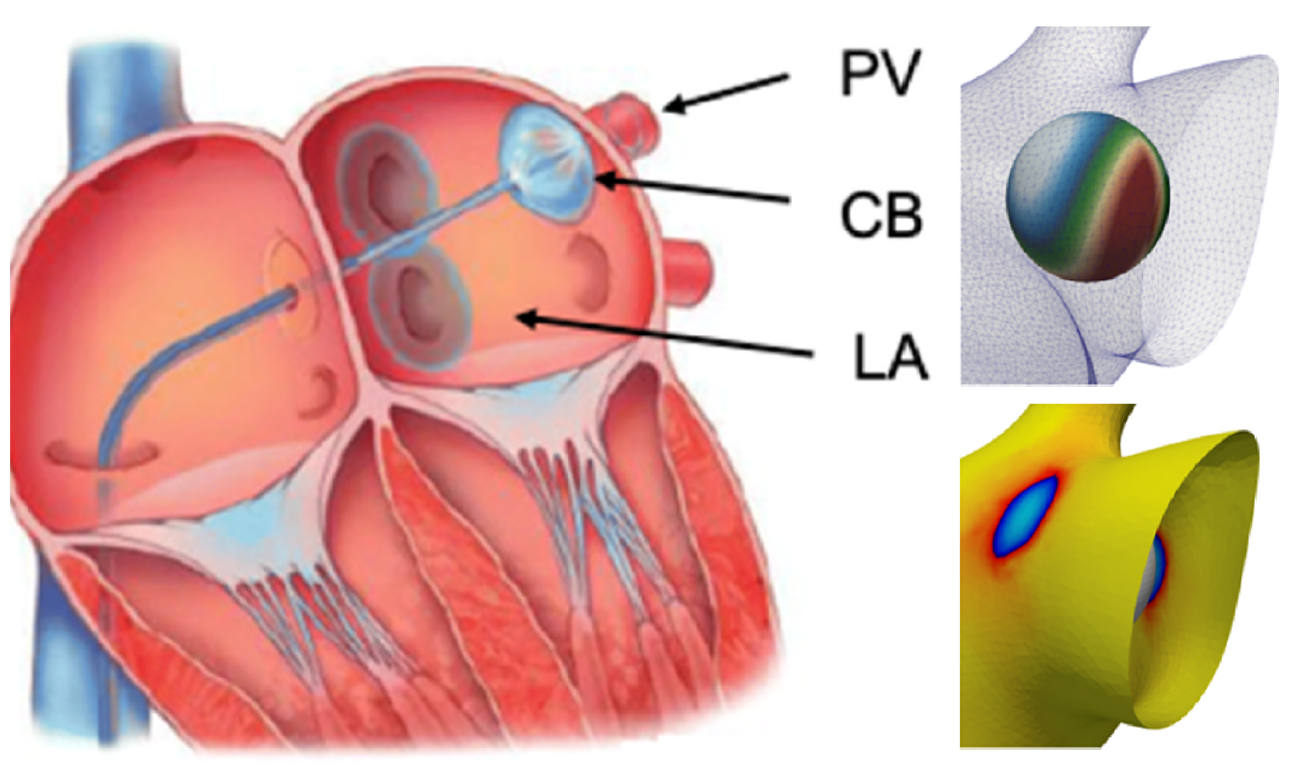
Fig 9: Simulation of CBA in a patient-specific case
( Patel et al. 2023).
5.  High-performance computing tools
Advances in computational technologies and the growth of open-source software have ushered in a new era of high-performance computing (HPC), transforming fundamental research in physical sciences and engineering by enabling data-driven approaches and machine learning. Given the complexity and high computational cost of fluid–structure interaction (FSI), emerging HPC tools now allow us to conduct 'thought experiments' across multiple spatial and temporal scales.
* Particle simulator   We introduce a complementarity-based collision resolution algorithm for smooth, non-spherical rigid bodies that avoids the scalability issues of traditional discrete surface methods. Instead of using numerous constraints between finely tessellated elements, our adaptive method solves a recursively generated linear complementarity problem (ReLCP) to identify collision points on the fly. We prove existence and uniqueness of the solution for strictly convex bodies and show convergence to classical methods at small timesteps. Our approach requires 10–100x fewer constraints than discrete methods, enabling high-fidelity simulations with up to 100x speedup. We validate its accuracy and scalability across several challenging scenarios. The algorhm forms the backbone of our new large scale particle simulator for nonlocal multibody dynamics (Mundy). The object-oriented open-source codes are built upon Sandia national lab's SIERRA Toolkit and Trilinos.
Fig 10: Examples of dense particle simulations in both quasi-2D and 3D using ReLCP ( Palmer et al. 2025 ).
* PDE solvers   Besides the discrete particle simulators, we solve PDE-based models using both in-house codes and powerful open-source parallel platforms including FEniCS and Dedalus, as well as commercial softwares.